2. Trigonometric Substitutions

Exercises

a. Substitutions for \(x^2+1\) and \(x^2-1\)

Evaluate each integral.

\( \displaystyle \int \dfrac{\sqrt{x^{2}-1}}{x}\,dx \)

\(\sec(u)=x\)

\( \displaystyle \int \dfrac{\sqrt{x^{2}-1}}{x}\,dx=\sqrt{x^{2}-1}-\text{arcsec}x+C \)

Use the trigonometric substitution \(x=\sec(u)\). Then \(dx=\tan(u)\sec(u)\,du\). \[\begin{aligned} \int\dfrac{\sqrt{x^2-1}}{x}\,dx &=\int\dfrac{\tan(u)}{\sec(u)}\tan(u)\sec(u)\,du \\ &=\int\tan^2(u)\,du \\ &=\int(\sec^2(u)-1)\,du \\ &=\tan(u)-u+C \\ &=\sqrt{x^2-1}-\text{arcsec}(x)+C \end{aligned}\]

pm

To check, we take the derivative. \[\begin{aligned} \left(\sqrt{x^2-1}-\text{arcsec}(x)\right)'&=2x\dfrac{1}{2\sqrt{x^2-1}}-\dfrac{1}{x\sqrt{x^2-1}} \\ &=\dfrac{x^2}{x\sqrt{x^2-1}}\,-\,\dfrac{1}{x\sqrt{x^2-1}} \\ &=\dfrac{x^2-1}{x\sqrt{x^2-1}} \\ &=\dfrac{\sqrt{x^2-1}}{x} \end{aligned}\]
\(\displaystyle\int\dfrac{x}{\left(x^2+1\right)^{3/2}}\,dx\)

Use the ordinary substitution \(u=x^2+1\).

\(\displaystyle\int\dfrac{x}{\left(x^2+1\right)^{3/2}}\,dx =-\dfrac{1}{\sqrt{x^2+1}}+C\)

Use the ordinary substitution \(u=x^2+1\). Then \(du=2x\,dx\) or \(\dfrac{1}{2}\,du=x\,dx\). So: \[\begin{aligned} \int \dfrac{x}{(x^2+1)^{3/2}}\,dx &=\dfrac{1}{2}\int u^{-3/2}\,du \\ &=\dfrac{1}{2}(-2)u^{-1/2}+C =-\,\dfrac{1}{\sqrt{u}}+C \\ &=-\,\dfrac{1}{\sqrt{x^2+1}}+C \end{aligned}\]

vm,pm

We check by differentiating. If \(f(x)=-\dfrac{1}{\sqrt{x^2+1}}\) then: \[ f'(x)=\dfrac{1}{2}\dfrac{1}{(x^2+1)^{3/2}}(2x) =\dfrac{x}{(x^2+1)^{3/2}} \] which is the original integrand.
\( \displaystyle \int \dfrac{x}{\sqrt{x^{2}+1}}\,dx \)

Use the simpler method, \(u\)-substitution...

\( \displaystyle \int \dfrac{x}{\sqrt{x^{2}+1}}\,dx=\sqrt{x^{2}+1}+C \)

We use the ordinary substitution \(u=x^2+1\). Then \(du=2x\,dx\) or \(\dfrac{1}{2}\,du=x\,dx\). So: \[\begin{aligned} \int \dfrac{x}{\sqrt{x^{2}+1}}\,dx&=\dfrac{1}{2}\int u^{-1/2}\,du \\ &=\dfrac{1}{2}(2)u^{1/2}+C \\ &=\dfrac{1}{\sqrt{u}}+C \\ &=\sqrt{x^2+1}+C \\ \end{aligned}\]

pm

Check by differentiating. \[\begin{aligned} (\sqrt{x^2+1})'&=\dfrac{1}{2\sqrt{x^2+1}}(x^2+1)' \\ &=\dfrac{2x}{2\sqrt{x^2+1}} \\ &=\dfrac{x}{\sqrt{x^2+1}} \end{aligned}\]
\( \displaystyle \int \dfrac{5x-4}{\sqrt{1-x^{2}}}\,dx \)

Use the substitution \(x=\sin(\theta)\).

\( \displaystyle \int \dfrac{5x-4}{\sqrt{1-x^{2}}}\,dx=-5\sqrt{1-x^{2}}-4\arcsin x+C\)

We use the trigonometric substitution \(x=\sin(u)\). Then \(dx=\cos(u)\,du\). So: \[\begin{aligned} \displaystyle \int \dfrac{5x-4}{\sqrt{1-x^{2}}}\,dx &= \displaystyle \int \dfrac{5\sin(u)-4}{\sqrt{1-\sin^2u}}\cos(u)\,du \\ &= \displaystyle \int (5\sin(u)-4)\,du \\ &= -5\cos(u)-4u+C \\ &= -5\sqrt{1-x^2}-4\arcsin(x)+C \\ \end{aligned}\]
pm

Check by differentiating. If \(f=-5\sqrt{1-x^2}-4\arcsin(x)\), then \[\begin{aligned} f'&=-5\dfrac{(1-x^2)'}{2\sqrt{1-x^2}}-4\dfrac{1}{\sqrt{1-x^2}} \\ &=-5\dfrac{-2x}{2\sqrt{1-x^2}}-\dfrac{4}{\sqrt{1-x^2}} \\ &=\dfrac{5x-4}{\sqrt{1-x^2}} \end{aligned}\]

Verify the antiderivative formula: \(\displaystyle \int \dfrac{\sqrt{1-x^{2} }}{x^{4}}\,dx=-\,\dfrac{(1-x^2)^{3/2}}{3x^3}+C \)

Remember to verify an antiderivative requires only a derivative!

To verify the antiderivative, we let \(f=-\,\dfrac{(1-x^2)^{3/2}}{3x^3}\) and differentiate: \[\begin{aligned} f'&=-\,\dfrac{(3x^3)[(1-x^2)^{3/2}]'-(1-x^2)^{3/2}[3x^3]'}{(3x^3)^2} \\ &=-\dfrac{3x^3\dfrac{3}{2}(1-x^2)^{1/2}(-2x)-(1-x^2)^{3/2}9x^2}{9x^6} \\ &=-\,\dfrac{-9x^4\sqrt{1-x^2}-9x^2(1-x^2)\sqrt{1-x^2}}{9x^6} \\ &=-\,\dfrac{(-9x^4-9x^2+9x^4)\sqrt{1-x^2}}{9x^6} \\ &=\dfrac{\sqrt{1-x^2}}{x^4} \end{aligned}\] which is the integrand.
pm

Plot the parametric curve \((x,y)=\left(\theta\cos \theta,\theta\sin \theta\right)\) from \(\theta=\dfrac{-3\pi}{2}\) to \(\theta=\dfrac{3\pi}{2}\) and compute its arc length.

The formula for the arc length of a polar curve is given in the chapter on Polar Coordinates . It is \[ L=\int_\alpha^\beta \sqrt{r(\theta)^2+\left(\dfrac{dr}{d\theta}\right)^2}\,d\theta \] Since \(\theta\) is the variable of integration, you cannot use \(\theta\) as the new variable in the trig substitution.

Happy Valentine's Day!
\(\begin{aligned} L&=\dfrac{3\pi}{4}\sqrt{9\pi^2+4} +\dfrac{1}{2}\ln\dfrac{\sqrt{9\pi^2+4}+3\pi}{\sqrt{9\pi^2+4}-3\pi} \\ &\approx24.96 \end{aligned}\)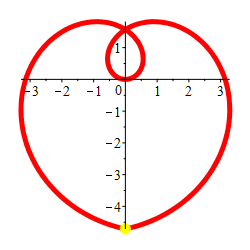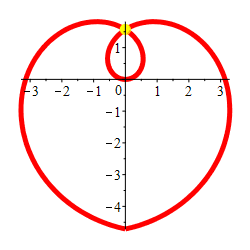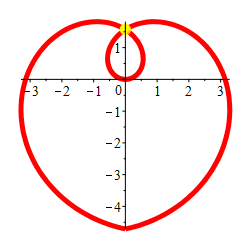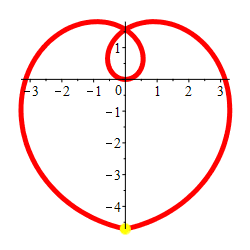

Comparing the curve \((x,y)=\left(\theta\cos \theta,\theta\sin \theta\right)\) to polar coordinates \((x,y)=\left(r\cos \theta,r\sin \theta\right)\), we see this is the polar curve \(r=\theta\). So the radius gets larger as the angle gets larger. It is a spiral as shown. Happy Valentine's Day!

The arc length of a polar curve is given by: \[ L=\int_\alpha^\beta \sqrt{r(\theta)^2+\left(\dfrac{dr}{d\theta}\right)^2}\,d\theta \] Here \(r=\theta\) and \(\dfrac{dr}{d\theta}=1\) and the limits are \(\alpha=-\,\dfrac{3\pi}{2}\) and \(\beta=\dfrac{3\pi}{2}\). So \[ L=\int_{-3\pi/2}^{3\pi/2} \sqrt{\theta^2+1}\,d\theta \]

We make the trig substitution \(\theta=\tan(u)\). Then \(d\theta=\sec^2(u)\,du\). So \[\begin{aligned} L&=\int_{\theta=-3\pi/2}^{3\pi/2} \sqrt{\tan^2 u+1}\sec^2(u)\,du \\ &=\int_{\theta=-3\pi/2}^{3\pi/2} \sec^3(u)\,du \\ \end{aligned}\] This indefinite integral was computed in the chapter on Trig Integrals. \[ L=\left[\dfrac{1}{2}\sec(u)\tan(u) +\dfrac{1}{2}\ln|\sec(u)+\tan(u)|\right]_{\theta=-3\pi/2}^{3\pi/2} \] To substitute back, we look at a triangle with angle \(u\), opposite side \(\theta\), adjacent side \(1\) and hypotenuse \(\sqrt{\theta^2+1}\): \[\begin{aligned} L&=\left[\dfrac{1}{2}\sqrt{\theta^2+1}\,\theta +\dfrac{1}{2}\ln|\sqrt{\theta^2+1}+\theta|\right]_{-3\pi/2}^{3\pi/2} \\ &=\dfrac{1}{2}\sqrt{\left(\dfrac{3\pi}{2}\right)^2+1}\,\dfrac{3\pi}{2} +\dfrac{1}{2}\ln\left|\sqrt{\left(\dfrac{3\pi}{2}\right)^2+1}+\dfrac{3\pi}{2}\right| \\ &\quad +\dfrac{1}{2}\sqrt{\left(\dfrac{3\pi}{2}\right)^2+1}\,\dfrac{3\pi}{2} -\dfrac{1}{2}\ln\left|\sqrt{\left(\dfrac{3\pi}{2}\right)^2+1}-\dfrac{3\pi}{2}\right| \\ &=\sqrt{\left(\dfrac{3\pi}{2}\right)^2+1}\,\dfrac{3\pi}{2} +\dfrac{1}{2}\ln\dfrac{\sqrt{\left(\dfrac{3\pi}{2}\right)^2+1}+\dfrac{3\pi}{2}} {\sqrt{\left(\dfrac{3\pi}{2}\right)^2+1}-\dfrac{3\pi}{2}} \\ &=\dfrac{\sqrt{9\pi^2+4}}{2}\,\dfrac{3\pi}{2} +\dfrac{1}{2}\ln\dfrac{\dfrac{\sqrt{9\pi^2+4}}{2}+\dfrac{3\pi}{2}} {\dfrac{\sqrt{9\pi^2+4}}{2}-\dfrac{3\pi}{2}} \\ &=\dfrac{3\pi}{4}\sqrt{9\pi^2+4} +\dfrac{1}{2}\ln\dfrac{\sqrt{9\pi^2+4}+3\pi}{\sqrt{9\pi^2+4}-3\pi} \\ &\approx 24.96 \end{aligned}\]

pm

b. Substitutions for \(a^2 x^2+b^2\) and \(a^2 x^2-b^2\)

Evaluate each integral.

\( \displaystyle \int \dfrac{dx}{\sqrt{x^{2}-4}}\)

Let \( x=2 \sec \theta \).

\( \displaystyle \int \dfrac{dx}{\sqrt{x^{2}-4}} =\ln \left\vert \dfrac{x}{2}+\dfrac{\sqrt{x^{2}-4}}{2}\right\vert+K =\ln\left|x+\sqrt{x^2-4}\right|+C \)

We let \(x=2\sec\theta\). So \(dx=2\sec\theta\tan\theta\,d\theta\). Then \[\begin{aligned} \int\dfrac{dx}{\sqrt{x^{2}-4}} &=\int\dfrac{2\sec\theta\tan\theta\,d\theta}{\sqrt{4\sec^2\theta-4}} =\int\dfrac{2\sec\theta\tan\theta\,d\theta}{\sqrt{4\tan^2\theta}} \\ &=\int\sec\theta\,d\theta=\ln|\sec\theta+\tan\theta|+K \end{aligned}\] Now we must express our result in terms of \(x\). Since \(\sec\theta=\dfrac{x}{2}\), we have: \[ \tan\theta=\sqrt{\sec^2\theta-1}=\sqrt{\dfrac{x^2}{4}-1} =\dfrac{\sqrt{x^2-4}}{2} \] Making these substitutions gives \[\begin{aligned} \int\dfrac{dx}{\sqrt{x^{2}-4}} &=\ln\left|\dfrac{x}{2}+\dfrac{\sqrt{x^2-4}}{2}\right|+K \\ &=\ln\left|\dfrac{x+\sqrt{x^2-4}}{2}\right|+K \\ &=\ln\left|x+\sqrt{x^2-4}\right|-\ln(2)+K \\ &=\ln\left|x+\sqrt{x^2-4}\right|+C \end{aligned}\]

pm

We check by differentiating: \[\begin{aligned} \dfrac{d}{dx}&\left(\ln\left|x+\sqrt{x^2-4}\right|\right) =\dfrac{\dfrac{d}{dx\rule[-2pt]{0pt}{10pt}}\left(x+\sqrt{x^2-4}\right)}{x+\sqrt{x^2-4}} \\ &=\dfrac{1+\dfrac{1}{2}\left[(x^2-4)^{-1/2}\right]2x}{x+\sqrt{x^2-4}} \\ &=\dfrac{1+\dfrac{x}{\sqrt{x^2-4}}}{\;\;x+\sqrt{x^2-4}\;\;} =\dfrac{\dfrac{\sqrt{x^2-4}+x}{\sqrt{x^2-4}}}{\;\;x+\sqrt{x^2-4}\;\;} \\ &=\dfrac{\sqrt{x^2-4}+x}{\sqrt{x^2-4}[x+\sqrt{x^2-4}]} =\dfrac{1}{\sqrt{x^2-4}} \end{aligned}\]
\(\displaystyle \int \dfrac{dx}{\sqrt{9-16x^{2}}}\)

Let \(x=\dfrac{3}{4}\sin(\theta)\).

\( \displaystyle \int \dfrac{dx}{\sqrt{9-16x^{2}}} =\dfrac{1}{4}\arcsin\left(\dfrac{4}{3}x\right)+C\)

Let \(x=\dfrac{3}{4}\sin(\theta)\). Then \(dx=\dfrac{3}{4}\cos(\theta)\,d\theta\). So: \[\begin{aligned} \int &\dfrac{dx}{\sqrt{9-16x^2}} =\int \dfrac{1}{\sqrt{9-9\sin^2(\theta)}}\dfrac{3}{4}\cos(\theta)\,d\theta =\int \dfrac{1}{3\cos(\theta)}\dfrac{3}{4}\cos(\theta)\,d\theta \\ &=\int \dfrac{1}{4}\,d\theta =\dfrac{\theta}{4}+C =\dfrac{1}{4}\arcsin\left(\dfrac{4}{3}x\right)+C \end{aligned}\]

pm

\[\begin{aligned} \dfrac{d}{dx}\dfrac{1}{4}\arcsin\left(\dfrac{4}{3}x\right) &=\dfrac{1}{4}\left[\dfrac{4}{3}\dfrac{1}{\sqrt{1-\left(\dfrac{4}{3}x\right)^2}}\right] \\ &=\dfrac{1}{3}\dfrac{1}{\sqrt{\dfrac{9-16x^2}{9}}} \\ &=\dfrac{1}{3}\dfrac{3}{\sqrt{9-16x^2}} \\ &=\dfrac{1}{\sqrt{9-16x^2}} \end{aligned}\]

An alternate way to do this problem is to make the ordinary substitution \(x=\dfrac{3}{4}u\). Then \(dx=\dfrac{3}{4}\,du\). So: \[\begin{aligned} \int \dfrac{dx}{\sqrt{9-16x^2}} &=\int \dfrac{1}{\sqrt{9-9u^2}}\dfrac{3}{4}\,du \\ &=\dfrac{1}{4}\int \dfrac{1}{\sqrt{1-u^2}}\,du \\ &=\dfrac{1}{4}\arcsin(u)+C \\ &=\dfrac{1}{4}\arcsin\left(\dfrac{4}{3}x\right)+C \end{aligned}\]
\( \displaystyle \int \dfrac{x^{3}}{\sqrt{9x^{2}+49}}\,dx \)

Do the normal substitution \(u=9x^2+49\).

\( \displaystyle \int \dfrac{x^{3}}{\sqrt{9x^{2}+49}}\,dx\) \(\quad =\dfrac{1}{243}(9x^{2}+49)^{3/2}-\dfrac{49}{81}\sqrt{9x^{2}+49}+C \)

We use the ordinary substitution \(u=9x^{2}+49\) so that \(du=18x\,dx\) and \(x^2=\dfrac{u-49}{9}\). Then: \[\begin{aligned} \int\dfrac{x^3}{\sqrt{9x^2+49}}\,dx &=\int x^2\dfrac{1}{\sqrt{9x^2+49}}x\,dx \\ &=\int\dfrac{u-49}{9}\dfrac{1}{\sqrt{u}}\dfrac{du}{18} \\ &=\dfrac{1}{162}\int\left(\sqrt{u}-\dfrac{49}{\sqrt{u}}\right)\,du \\ &=\dfrac{1}{162}\dfrac{2u^{3/2}}{3}-\dfrac{49}{162}2\sqrt{u}+C \\ &=\dfrac{1}{243}\left(9x^{2}+49\right)^{3/2}-\dfrac{49}{81}\sqrt{9x^{2}+49}+C \end{aligned}\]

vm,pm

We check by differentiating. If \(f(x)=\dfrac{1}{243}\left(9x^{2}+49\right)^{3/2}-\dfrac{49}{81}\sqrt{9x^{2}+49}\), then \[\begin{aligned} f'(x)&=\dfrac{1}{243}\dfrac{3}{2}(9x^2+49)^{1/2}[18x] -\dfrac{49}{81}\dfrac{1}{2\sqrt{9x^2+49}}[18x] \\ &=\dfrac{x}{9}\sqrt{9x^2+49}-\dfrac{49x}{9\sqrt{9x^2+49}} \\ &=\dfrac{x(9x^2+49)-49x}{9\sqrt{9x^2+49}} =\dfrac{9x^3+49x-49x}{9\sqrt{9x^2+49}} \\ &=\dfrac{x^3}{\sqrt{9x^2+49}} \end{aligned}\]

We can also do the integral by a trig substitution. Let \(x=\dfrac{7}{3}\tan(\theta)\), which implies \(dx=\dfrac{7}{3}\sec^2(\theta)\,d\theta\). Then \[\begin{aligned} \int \dfrac{x^3}{\sqrt{9x^2+49}}\,dx &=\int \dfrac{\dfrac{343}{27}\tan^3(\theta)}{\sqrt{49\tan^2\theta+49}}\dfrac{7}{3}\sec^2(\theta)\,d\theta \\ &=\dfrac{343}{81}\int \dfrac{\tan^3(\theta)\sec^2(\theta)}{\sqrt{\sec^2\theta}}\,d\theta \\ &=\dfrac{343}{81}\int \tan^3(\theta)\sec(\theta)\,d\theta \\ &=\dfrac{343}{81}\int (\sec^2(\theta)-1)\tan(\theta)\sec(\theta)\,d\theta \end{aligned}\] Then let \(u=\sec(\theta)\). Then \(du=\sec(\theta)\tan(\theta)d\theta\). \[\begin{aligned} \int \dfrac{x^3}{\sqrt{9x^2+49}}\,dx &=\dfrac{343}{81}\int (u^2-1)\,du \\ &=\dfrac{343}{81}\left[\dfrac{u^3}{3}-u\right]+C \end{aligned}\] Since \(u=\sec(\theta)=\sqrt{\tan^2{\theta}+1}=\dfrac{\sqrt{9x^2+49}}{7}\), we have: \[\begin{aligned} \int \dfrac{x^3}{\sqrt{9x^2+49}}\,dx &=\dfrac{343}{81}\left[\dfrac{(9x+49)^{3/2}}{3 \cdot 343}-\dfrac{\sqrt{9x^2+49}}{7}\right]+C \\ &=\dfrac{1}{243}\left(9x^{2}+49\right)^{3/2}-\dfrac{49}{81}\sqrt{9x^{2}+49}+C \end{aligned}\]
pm
\( \displaystyle \int_{0}^{6}\sqrt{36-x^{2}}\,dx \)

A trig substitution will work, but recognizing the geometric figure makes the problem especially simple.

\( \displaystyle \int_{0}^{6}\sqrt{36-x^{2}}\,dx = 9\pi\)

The graph of \(y=36-x^2\) for \(0 \le x \le 6\) is a quarter circle with radius \(6\). The area of the whole circle is \(\pi \cdot 6^2 = 36\pi\), so a quarter of it would have an area \[ \int_{0}^{6}\sqrt{36-x^{2}}\,dx = A =\dfrac{1}{4}36\pi= 9\pi \]
pm

The integral can also be computed by the trig substitution \(x=6\sin(\theta)\), which means \(dx\,=6\cos(\theta)\,d\theta\). \[\begin{aligned} \displaystyle \int_0^6 \sqrt{36-x^2} \,dx &= \int_0^{\pi/2} \sqrt{36-36\sin^2(\theta)}\,6\cos(\theta)\,d\theta \\ &=36\int_0^{\pi/2} \sqrt{1-\sin^2(\theta)}\cos(\theta)\,d\theta \\ &=36\int_0^{\pi/2} \cos^2(\theta)\,d\theta \\ &=36\int_0^{\pi/2} \dfrac{1+\cos(2\theta)}{2}\,d\theta \\ &=18\int_0^{\pi/2} 1+\cos(2\theta)\,d\theta\\ &=18\left[\theta+\dfrac{\sin2\theta}{2}\right]_0^{\pi/2} =9\pi \end{aligned}\] Notice this solution was harder than using geometry.

pm

Find the arc length of the portion of \(y=x^{2}\) on the interval \(\left[ 0,\dfrac{\sqrt{3}}{2}\right]\)

Let \(x=\dfrac{1}{2}\tan(\theta)\).

\( \displaystyle L=\int_{0}^{\sqrt{3}/2} \sqrt{1+4x^{2}}\,dx=\dfrac{1}{2}\sqrt{3}+\dfrac{1}{4} \ln \left( 2+\sqrt{3}\right) \)

\[\begin{aligned} L&=\int_a^b \sqrt{1+\left(\dfrac{dy}{dx} \right )^2}\,dx \\ &=\int_{0}^{\sqrt{3}/2}\sqrt{1+4x^{2}}\,dx \end{aligned}\] Let \(x=\dfrac{1}{2}\tan(\theta)\). Then \(dx=\dfrac{1}{2}\sec^2(\theta)\,d\theta\). \[\begin{aligned} L&=\int_{x=0}^{\sqrt{3}/2}\sqrt{1+\tan^2(\theta)}\,\dfrac{\sec^2(\theta)}{2}\,d\theta \\ &=\dfrac{1}{2}\int_{x=0}^{\sqrt{3}/2}\sec^3(\theta)\,d\theta \\ \end{aligned}\] We found this integral in the chapter on Trig Integrals: \[ L=\dfrac{1}{2}\left[\dfrac{1}{2}\sec(\theta)\tan(\theta) +\dfrac{1}{2}\ln|\sec(\theta)+\tan(\theta)|\right]_{x=0}^{\sqrt{3}/2} \] Since \(\tan(\theta)=2x\), we know \(\sec(\theta)=\sqrt{4x^2+1}\). So: \[\begin{aligned} L&=\dfrac{1}{4}\left[\sqrt{4x^2+1}\,2x+\ln|\sqrt{4x^2+1}+2x|\right]_{x=0}^{\sqrt{3}/2}\\ &=\dfrac{1}{4}\sqrt{3+1}\sqrt{3}+\dfrac{1}{4}\ln|\sqrt{3+1}+\sqrt{3}|\\ &\quad-\,\dfrac{1}{4}\sqrt{1}\,\cdot 0-\dfrac{1}{4}\ln|\sqrt{1}+0|\\ &=\dfrac{1}{2}\sqrt{3}+\dfrac{1}{4}\ln\left(2+\sqrt{3}\right) \end{aligned}\]

gk,pm

c. Completing Squares

Complete the squares in each of these. Then integrate using trig substitutions.

\(\displaystyle \int \dfrac{dx}{\sqrt{x^{2}-2x+5}}\)

Let \(x-1=2\tan{\theta}\).

\(\displaystyle \int\dfrac{dx}{\sqrt{x^2-2x+5}} =\ln\left|\sqrt{x^2-2x+5}+x-1\right|+C \)

We complete the square: \[ \int\dfrac{dx}{\sqrt{x^2-2x+5}} =\int\dfrac{dx}{\sqrt{x^2-2x+1+4}} =\int\dfrac{dx}{\sqrt{(x-1)^2+4}} \] Now let \(x-1=2\tan\theta\). Then \(dx=2\sec^2\theta\,d\theta\) and: \[ \sqrt{(x-1)^2+4}=\sqrt{4\tan^2\theta +4} =\sqrt{4\sec^2\theta}=2\sec\theta \] We now rewrite the integral: \[\begin{aligned} \int &\dfrac{dx}{\sqrt{x^2-2x+5}} =\int\dfrac{2\sec^2\theta\,d\theta}{2\sec\theta} \\ &=\int\sec\theta\,d\theta =\ln|\sec\theta+\tan\theta|+C \end{aligned}\] Finally, to obtain our result in terms of \(x\), we could draw a right triangle or use the formulas: \[\begin{aligned} \tan\theta&=\dfrac{x-1}{2} \\ \sec\theta&=\sqrt{\tan^2\theta+1} =\sqrt{\dfrac{(x-1)^2}{4}+1} \\ &=\dfrac{\sqrt{(x-1)^2+4}}{2} \end{aligned}\] Putting all this together, we get \[\begin{aligned} \int\dfrac{dx}{\sqrt{x^2-2x+5}} &=\ln\left|\dfrac{\sqrt{x^2-2x+5}}{2}+\dfrac{x-1}{2}\right| +C_1 \\ &=\ln\left|\sqrt{x^2-2x+5}+x-1\right| +C \end{aligned}\]

vm,pm

\[\begin{aligned} \dfrac{d}{dx}&\ln\left|\sqrt{x^2-2x+5}+x-1\right| =\dfrac{\dfrac{2x-2}{2\sqrt{x^2-2x+5}}+1}{\sqrt{x^2-2x+5}+x-1} \\ &\quad=\dfrac{x-1+\sqrt{x^2-2x+5}} {\sqrt{x^2-2x+5}\left(\sqrt{x^2-2x+5}+x-1\right)} \\ &\quad=\dfrac{1}{\sqrt{x^2-2x+5}} \end{aligned}\]
\(\displaystyle \int \dfrac{x-1}{\sqrt{x^{2}-4x+3}}\,dx\)

Let \(x-2=\sec(\theta)\).

\(\displaystyle \int \dfrac{x-1}{\sqrt{x^{2}-4x+3}}\,dx =\sqrt{x^2-4x+3}+\ln\left|x-2+\sqrt{x^2-4x+3}\right|+C\)

We first complete the square: \[ \int \dfrac{x-1}{\sqrt{x^{2}-4x+3}}\,dx =\int \dfrac{x-1}{\sqrt{(x-2)^2-1}}\,dx \] Now let \(x-2=\sec\theta\). Then \(dx=\sec{\theta}\tan{\theta}\,d\theta\). So: \[\begin{aligned} \int \dfrac{x-1}{\sqrt{x^{2}-4x+3}}\,dx &=\int \dfrac{\sec{\theta}+2-1}{\tan{\theta}}\sec{\theta}\tan{\theta}\,d\theta \\ &=\int \sec^2{\theta}+\sec{\theta}\,d\theta \\ &=\tan{\theta}+\ln|\sec{\theta}+\tan{\theta}| +C \\ &=\sqrt{\sec^2{\theta}-1}+\ln\left|\sec{\theta}+\sqrt{\sec^2{\theta}-1}\right|+C \\ &=\sqrt{x^2-4x+3}+\ln\left|x-2+\sqrt{x^2-4x+3}\right|+C \end{aligned}\]

pm

\[\begin{aligned} \dfrac{d}{dx}&\left(\sqrt{x^2-4x+3}+\ln\left|x-2+\sqrt{x^2-4x+3}\right|\right) \\ &=\dfrac{2x-4}{2\sqrt{x^2-4x+3}}+\dfrac{1+\dfrac{2x-4}{2\sqrt{x^2-4x+3}}}{\;x-2+\sqrt{x^2-4x+3}\;} \\ &=\dfrac{x-2}{\sqrt{x^2-4x+3}}+\dfrac{\dfrac{x-2+\sqrt{x^2-4x+3}}{\sqrt{x^2-4x+3}}}{\;\;x-2+\sqrt{x^2-4x+3}\;\;} \\ &=\dfrac{x-2}{\sqrt{x^2-4x+3}}+\dfrac{1}{\sqrt{x^2-4x+3}} \\ &=\dfrac{x-1}{\sqrt{x^2-4x+3}}\\ \end{aligned}\]
\(\displaystyle \int \dfrac{x}{\sqrt{5+4x-x^{2}}}\,dx\)

Complete the square and let \(x-2=3\sin\theta\).

\(\displaystyle \int \dfrac{x}{\sqrt{5+4x-x^{2}}}\,dx =-\sqrt{5+4x-x^2}+2\arcsin{\dfrac{x-2}{3}}+C\)

We complete the square: \[ \int \dfrac{x}{\sqrt{5+4x-x^2}}\,dx =\int \dfrac{x}{\sqrt{9-(x^2-4x+4)}}\,dx =\int \dfrac{x}{\sqrt{9-(x-2)^2}}\,dx \] Now let \(x-2=3\sin\theta\). Then \(dx=3\cos\theta\,d\theta\) and: \[ \sqrt{9-(x-2)^2}=\sqrt{9-9\sin^2\theta} =\sqrt{9\cos^2\theta}=3\cos\theta \] Putting it all together, we get: \[\begin{aligned} \int \dfrac{x}{\sqrt{5+4x-x^2}}\,dx &=\int \dfrac{(3\sin\theta+2)}{3\cos\theta}3\cos\theta\,d\theta \\ &=\int 3\sin\theta+2\,d\theta \\ &=-3\cos\theta+2\theta+C \\ \end{aligned}\] Since \(\sin\theta=\dfrac{x-2}{3}\), we have \(\theta=\arcsin\dfrac{x-2}{3}\) and \[ \cos\theta=\sqrt{1-\sin^2\theta} =\sqrt{1-\dfrac{(x-2)^2}{9}} =\dfrac{\sqrt{9-(x-2)^2}}{3} \] Consequently: \[\begin{aligned} \int \dfrac{x}{\sqrt{5+4x-x^2}}\,dx &=-3\,\dfrac{\sqrt{9-(x-2)^2}}{3}+2\arcsin{\dfrac{x-2}{3}}+C \\ &=-\sqrt{5+4x-x^2}+2\arcsin{\dfrac{x-2}{3}}+C \end{aligned}\]

vm,pm

\[\begin{aligned} \dfrac{d}{dx}&\left(-\sqrt{5+4x-x^2}+2\arcsin\left(\dfrac{x-2}{3}\right)\right) \\ &=-\dfrac{4-2x}{2\sqrt{5+4x-x^2}}+2\dfrac{\dfrac{1}{3}}{\sqrt{1-\dfrac{x^2-4x+4}{9}}} \\ &=\dfrac{x-2}{\sqrt{5+4x-x^2}}+\dfrac{2}{\sqrt{5+4x-x^2}} \\ &=\dfrac{x}{\sqrt{5+4x-x^2}} \end{aligned}\]

d. Hyperbolic Trig Substitutions (Optional)

Compute each of the following integrals using a hyperbolic trig substitution.

\(\displaystyle\int \dfrac{4}{\sqrt{x^2-1}}dx\)

Use the substitution \(x = \cosh \lambda\).

\(\displaystyle\int \dfrac{4}{\sqrt{x^2-1}}dx = 4\mathrm{arccosh}\,x + C = 4\ln\left(x+\sqrt{x^2-1}\right)+C\)

Let \(x = \cosh \lambda \). Thus,\( \,dx = \sinh \lambda\,d\lambda \). \[\begin{aligned} \int \dfrac{4}{\sqrt{x^2-1}}\,dx &= \int \dfrac{4}{\sqrt{\cosh^2\lambda - 1}}\sinh \lambda \,d\lambda \\ &= \int \dfrac{4}{\sqrt{\sinh^2\lambda}}\sinh \lambda \,d\lambda \\ &= \int 4 \,d\lambda \\ &= 4\lambda + C \\ \end{aligned}\] Next, we substitute back for \(x\). Since \(x = \cosh \lambda \), we know \(\lambda = \mathrm{arccosh}\,x \). Therefore, \[ \int \dfrac{4}{\sqrt{x^2-1}}\,dx = 4\,\mathrm{arccosh}\,x + C \] While this is a fine answer, \(\mathrm{arccosh}\,x\) can also be expressed using the formula \(\mathrm{arccosh}\,x = \ln\left(x+\sqrt{x^2-1}\right)\). So: \[ \int \dfrac{4}{\sqrt{x^2-1}}\,dx = 4\ln\left(x+\sqrt{x^2-1}\right) + C \]

las
\(\displaystyle\int \dfrac{x^2}{1-x^2}\,dx\)

Use the substitution \(x = \mathrm{tanh}\,\lambda\).

\( \displaystyle \int \dfrac{x^2}{1-x^2}\,dx = \mathrm{arctanh}\,x - x + C = \dfrac{1}{2}\ln\left(\dfrac{1+x}{1-x}\right) - x + C \)

Let \(x=\tanh\,\lambda\). Then \(dx=\mathrm{sech}^2\,\lambda\,\tanh\,\lambda\,d\lambda\). \[\begin{aligned} \int \dfrac{x^2}{1-x^2} \,dx &= \int\dfrac{\tanh^2\lambda}{1-\tanh^2\lambda}\, \mathrm{sech}^2\lambda\,d\lambda \\ &= \int \dfrac{\tanh^2\lambda}{\mathrm{sech}^2\,\lambda}\, \mathrm{sech}^2\lambda\,d\lambda \\ &= \int \tanh^2\lambda \,d\lambda \\ \end{aligned}\] Next, we use the identity \(\tanh^2 t = 1 - \mathrm{sech}^2\,t\). \[\begin{aligned} \int \dfrac{x^2}{1-x^2}\,dx &= \int 1 - \mathrm{sech}^2\,\lambda \,d\lambda\\ &= \lambda - \tanh\lambda + C \end{aligned}\] Finally, we substitute back for \(x\). Since \(x = \tanh\lambda\), we have \(\lambda = \mathrm{arctanh}\,x\). So: \[ \int \dfrac{x^2}{1-x^2}\,dx = \mathrm{arctanh}\,x - x + C \] While this is a fine answer, \(\mathrm{arctanh}\,x\) can also be expressed using the formula \(\mathrm{arctanh}\,x = \dfrac{1}{2}\ln\left(\dfrac{1+x}{1-x}\right)\). \[ \int \dfrac{x^2}{1-x^2}\,dx = \dfrac{1}{2}\ln\left(\dfrac{1+x}{1-x}\right) - x + C \]

las

This integral can also be done by subtracting and adding \(1\) from the numerator. \[\begin{aligned} \int \dfrac{x^2}{1-x^2} \,dx &=\int \dfrac{x^2-1+1}{1-x^2} \,dx \\ &=\int -1+\dfrac{1}{1-x^2} \,dx \\ &=-x+\mathrm{arctanh}\,x+C \end{aligned}\]
\(\displaystyle\int \dfrac{2x-12}{\sqrt{x^2+1}}\,dx\)

Use the substituation \(x = \sinh \lambda \)

\(\begin{aligned} \int \dfrac{2x-12}{\sqrt{x^2+1}}\,dx &=2\sqrt{1 + x^2}-12\,\mathrm{arcsinh}\,x + C \\ &=2\sqrt{1 + x^2}-12 \ln(x + \sqrt{x^2+1})+C \end{aligned}\)

We let \(x = \sinh \lambda\). Then \(dx = \cosh \lambda\,d\lambda\). \[\begin{aligned} \int \dfrac{2x-12}{\sqrt{x^2+1}}\,dx &= \int \dfrac{2\sinh\lambda-12}{\sqrt{\sinh^2\lambda+1}}\cosh\lambda \,d\lambda \\ &= \int (2\sinh\lambda-12) \,d\lambda \\ &= 2\cosh\lambda-12\lambda + C \\ \end{aligned}\] Finally, we use the identity \(\cosh\lambda = \sqrt{1+\sinh^2\lambda} = \sqrt{1+x^2}\) and \(\lambda = \mathrm{arcsinh}\,x\) to express the integral in terms of \(x\): \[ \int \dfrac{2x-12}{\sqrt{x^2+1}}\,dx = 2\sqrt{1 + x^2}-12\,\mathrm{arcsinh}\,x + C \] Although this is a fine answer, we can also write the answer without inverse hyperbolic functions. We know that \(\mathrm{arcsinh}\,x = \ln(x + \sqrt{x^2+1})\), thus: \[ \int \dfrac{2x-12}{\sqrt{x^2+1}}\,dx = 2\sqrt{1 + x^2}-12 \ln(x + \sqrt{x^2+1})+C \]

las
\(\displaystyle\int \dfrac{\sqrt{4x^2-9}}{x^2}\,dx\)

Use the substitution \(x = a\cosh\lambda\) with some constant \(a\).

\(\begin{aligned} \int \dfrac{\sqrt{4x^2-9}}{x^2} \,dx &=2\,\mathrm{arccosh}\,\dfrac{2x}{3} - 2\sqrt{1-\dfrac{9}{4x^2}} \\ &=2\ln\left(2x + \sqrt{4x^2-9}\right) - \dfrac{\sqrt{4x^2-9}}{x} + C \end{aligned}\)

We let \(4x^2=9\cosh^2\lambda\). Then \(x = \dfrac{3}{2}\cosh\lambda\) and thus, \(dx = \dfrac{3}{2}\sinh\lambda\,d\lambda\). Then: \[\begin{aligned} \int \dfrac{\sqrt{4x^2-9}}{x^2}\,dx &=\int \dfrac{\,\sqrt{9\cosh^2\lambda-9}\,}{\dfrac94\cosh^2\lambda} \,\dfrac{3}{2} \sinh\lambda\,d\lambda \\ &=2\int \dfrac{\sinh^2\lambda}{\cosh^2\lambda}\,d\lambda\\ &=2\int \mathrm{tanh}^2\,\lambda\,d\lambda \\ &=2\int (1 - \mathrm{sech}^2\,\lambda)\,d\lambda \\ &= 2\lambda - 2\mathrm{tanh}\,\lambda + C \end{aligned}\] Since \(x = \dfrac{3}{2}\cosh\lambda\), we have \(\lambda = \mathrm{arccosh}\,\dfrac{2x}{3}\) and \[\begin{aligned} \tanh \lambda &=\dfrac{\sinh\lambda}{\cosh\lambda} =\dfrac{\sqrt{\cosh^2\lambda-1}}{\cosh\lambda} \\ &=\dfrac{\sqrt{\dfrac{4x^2}{9}-1}}{\dfrac{2x}{3}} =\dfrac{\sqrt{4x^2-9}}{2x} \end{aligned}\] So the integral becomes: \[ \int \dfrac{\sqrt{4x^2-9}}{x^2}\,dx =2\,\mathrm{arccosh}\,\dfrac{2x}{3} - \dfrac{\sqrt{4x^2-9}}{x} + C \] Although this is a perfectly fine answer, we can also rewrite it without hyperbolic functions. Since \(\mathrm{arccosh}\,x =\ln\left(x + \sqrt{x^2-1}\right)\), we conclude \(\mathrm{arccosh}\,\dfrac{2x}{3} =\ln\left(\dfrac{2x}{3} + \sqrt{\dfrac{4x^2}{9}-1}\right)\). So: \[\begin{aligned} \int \dfrac{\sqrt{4x^2-9}}{x^2}\,dx &= 2\ln\left(\dfrac{2x}{3} + \dfrac{\sqrt{4x^2-9}}{3}\right) - \dfrac{\sqrt{4x^2-9}}{x} + C \\ &= 2\ln\left(2x + \sqrt{4x^2-9}\right) + 2\ln\left(\dfrac{1}{3}\right) - \dfrac{\sqrt{4x^2-9}}{x} + C \\ &= 2\ln\left(2x + \sqrt{4x^2-9}\right) - \dfrac{\sqrt{4x^2-9}}{x} + C' \end{aligned}\] where we have absorbed the \(2\ln\left(\dfrac{1}{3}\right)\) into the constant \(C'\). This simplification will be useful in the remark.

las

This integral can also be solved using an ordinary trig substitutions. In particular, let \(4x^2 =9\sec^2\theta\). Then, \(x = \dfrac{3}{2}\sec\theta\) and \(dx = \dfrac{3}{2}\sec\theta\tan\theta\,d\theta\). So: \[\begin{aligned} \int \dfrac{\sqrt{4x^2-9}}{x^2}\,dx &=\int \dfrac{\,\sqrt{9\sec^2\theta-9}\,}{\dfrac{9}{4}\sec^2\theta} \,\dfrac{3}{2}\sec\theta\tan\theta\,d\theta \\ &= 2\int \dfrac{\tan^2\theta}{\sec\theta} \,d\theta =2\int \dfrac{\sec^2\theta - 1}{\sec\theta} \,d\theta \\ &=2\int \sec\theta - \cos\theta d\theta \\ &= 2\ln|\sec\theta + \tan\theta| - 2\sin\theta + C \end{aligned}\] To express this in terms of \(x\), since \(\sec\theta=\dfrac{2x}{3}\), we draw a triangle with hypotenuse \(2x\), adjacent side \(3\), and opposite side \(\sqrt{4x^2-9}\). Then: \[\begin{aligned} \int \dfrac{\sqrt{4x^2-9}}{x^2}\,dx &=2\ln\left|\dfrac{2x}{3}+\sqrt{4x^2-9}\right| - \dfrac{\sqrt{4x^2-9}}{x} + C \end{aligned}\] This is the same as one step in the previous answer.

Find the area of the hyperbolic sector between the hyperbola \(x^2-y^2=1\), the \(x\)-axis and the line between the origin and the point \((\cosh\lambda,\sinh\lambda)\).

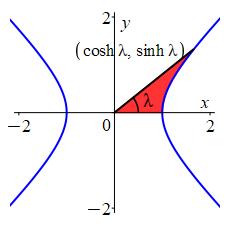
Instead of trying to calculate the area of the sector directly, find the area of the triangle and subtract the area below the curve.

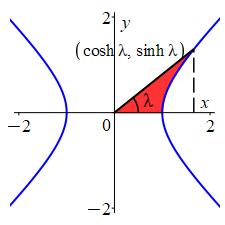
\(\displaystyle A_\text{sector}= \dfrac{1}{2} \lambda\)

To find for the area of the hyperbolic sector, we will first find the area of the triangle with vertices \((0,0),(\cosh\lambda,0), (\cosh\lambda, \sinh\lambda)\) and subtract the area below the hyperbola.

The area of the triangle is \[ A_\triangle=\dfrac12\,\text{base}\;\text{height} =\dfrac12 \cosh\lambda \sinh\lambda \] The area under the hyperbola is \[ A_\text{hyp}=\int_1^{\cosh\lambda} \sqrt{x^2-1}\,dx \] To integrate, we use the hyperbolic trig subtitution, \(x = \cosh t\). Then \(dx = \sinh t \,dt\). So: \[\begin{aligned} A_\text{hyp} &=\int_{x=1}^{\cosh\lambda}\sqrt{\cosh^2t - 1}\,\sinh t \,dt \\ &=\int_{x=1}^{\cosh\lambda} \sinh^2t \,dt \end{aligned}\] Next, we substitute \(\sinh^2t=\dfrac{1}{2}(\cosh{2t}-1)\): \[\begin{aligned} A_\text{hyp} &= \int_{x=1}^{\cosh\lambda}\dfrac{1}{2}( \cosh{2t}-1)\,dt \\ &= \dfrac{1}{2}\left[\dfrac{1}{2}\sinh{2t}-t\right]_{x=1}^{\cosh\lambda} \end{aligned}\] Before substituting back, we use the identity \(\sinh{2t}=2\cosh t\sinh t\): \[\begin{aligned} A_\text{hyp} &=\dfrac{1}{2}\left[\rule{0pt}{10pt}\cosh t\sinh t-t\right]_{x=1}^{\cosh\lambda} \\ &=\dfrac{1}{2}\left[\rule{0pt}{10pt}\cosh t\sqrt{\cosh^2 t-1}-t\right]_{x=1}^{\cosh\lambda} \end{aligned}\] To substitute back to \(x\) values, we use our definition \(\cosh t=x\) and also \(t = \mathrm{arccosh}\,x\), as well as \(\mathrm{arccosh}\,(1)=0\): \[\begin{aligned} A_\text{hyp} &=\dfrac{1}{2}\left[x\sqrt{x^2-1}-\mathrm{arccosh}\,x\right]_1^{\cosh\lambda} \\ &=\dfrac{1}{2}\cosh\lambda \sqrt{\cosh^2\lambda-1}-\dfrac{1}{2}\mathrm{arccosh}(\cosh\lambda)-0 \\ &=\dfrac{1}{2}\cosh\lambda \sinh\lambda-\dfrac{1}{2}\lambda \end{aligned}\] Finally, we combine this with the area of the triangle to get: \[\begin{aligned} A_\text{sector}&=A_\triangle-A_\text{hyp} \\ &= \dfrac{1}{2}\cosh\lambda \sinh\lambda - \left[ \dfrac{1}{2}\cosh\lambda \sinh\lambda-\dfrac{1}{2}\lambda\right] \\ &= \dfrac{1}{2}\lambda \end{aligned}\]

las

It's interesting compare the area of a hyperbolic sector to the area of a circlar sector. The full unit circle has area \(A_\bigcirc=\pi r^2=\pi\). The fraction inside the sector is \(\dfrac{\theta}{2\pi}\) where \(\theta\) is measured in radians. So the area of the sector is: \[ A_\measuredangle=\dfrac{\theta}{2\pi}\pi=\dfrac{1}{2}\theta \]

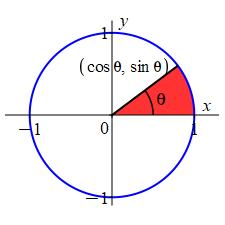
This relationship is the same as the hyperbolic area, \(A = \dfrac{1}{2}\lambda\).

Review Exercises

Evaluate using any appropriate method.

\(\displaystyle \int \dfrac{\sqrt{x^{2}-9}}{x}\,dx\)

Let \(x=3\sec(\theta)\).

\( \displaystyle \int \dfrac{\sqrt{x^{2}-9}}{x}\,dx=\sqrt{x^{2}-9}-3\text{arcsec}\dfrac{x}{3} +C\)

Let \(x=3\sec\theta\). Then \(dx=3\sec{\theta}\tan{\theta}\,d\theta\). \[\begin{aligned} \int \dfrac{\sqrt{x^{2}-9}}{x}\,dx &=\int \dfrac{\sqrt{9\sec^{2}{\theta}-9}}{3\sec\theta}\,3\sec\theta\tan\theta\,d\theta \\ &=\int 3\tan^2{\theta}\,d\theta \\ &=\int 3\sec^2{\theta}-3\,d\theta \\ &=3\tan{\theta}-3\,\theta+C \\ &=3\sqrt{\sec^2{\theta}-1}-3\,\text{arcsec}{\dfrac{x}{3}}+C \\ &=\sqrt{x^2-9}-3\,\text{arcsec}{\dfrac{x}{3}}+C \end{aligned}\]

pm

\[\begin{aligned} \dfrac{d}{dx}\left(\sqrt{x^{2}-9}-3\text{arcsec}\dfrac{x}{3}\right) &=\dfrac{2x}{2\sqrt{x^2-9}}-3{\dfrac{\dfrac{1}{3}}{\left(\dfrac{x}{3}\right){\sqrt{\left(\dfrac{x}{3}\right)^{2}-1}}}} \\ &=\dfrac{x}{\sqrt{x^2-9}}-\dfrac{9}{x{\sqrt{x^2-9}}} \\ &=\dfrac{x^2-9}{x\sqrt{x^2-9}} \\ &=\dfrac{\sqrt{x^2-9}}{x} \end{aligned}\]
\(\displaystyle \int \dfrac{dx}{\sqrt{x^{2}+2x}}\)

Complete the square and then let \(x+1=\sec(\theta)\).

\( \displaystyle \int \dfrac{dx}{\sqrt{x^{2}+2x}} =\ln\left|1+x+\sqrt{\left(x^{2}+2x\right)}\right|+C\)

We first complete the square: \[ x^2+2x=(x+1)^2-1 \] So we let \(x+1=\sec{\theta}\). Then \(dx=\tan{\theta}\sec{\theta}\,d\theta\). \[\begin{aligned} \int \dfrac{dx}{\sqrt{x^2+2x}} &=\int \dfrac{dx}{\sqrt{(x+1)^2-1}} \\ &=\int \dfrac{\tan{\theta}\sec{\theta}}{\tan{\theta}}\,d\theta \\ &=\int \sec{\theta}\,d\theta \\ &=\ln|\sec{\theta}+\tan{\theta}|+C \\ &=\ln|x+1+\sqrt{\sec^2{\theta}-1}|+C \\ &=\ln|x+1+\sqrt{(x+1)^2-1}|+C \\ &=\ln|x+1+\sqrt{x^2+2x}|+C \end{aligned}\]

pm

\[\begin{aligned} \dfrac{d}{dx}\ln|x+1+\sqrt{x^2+2x}| &=\dfrac{1+\dfrac{2x+2}{2\sqrt{x^2+2x}}}{x+1+\sqrt{x^2+2x}} \\ &=\dfrac{2\sqrt{x^2+2x}+2x+2}{2x\sqrt{x^2+2x}+2\sqrt{x^2+2x}+2x^2+4x} \\ &=\dfrac{\sqrt{x^2+2x}+x+1}{x\sqrt{x^2+2x}+\sqrt{x^2+2x}+x^2+2x} \\ &=\dfrac{x+1+\sqrt{x^2+2x}}{\sqrt{x^2+2x}(x+1+\sqrt{x^2+2x})} \\ &=\dfrac{1}{\sqrt{x^2+2x}} \end{aligned}\]
\(\displaystyle \int \dfrac{x}{\sqrt{9-x^{2}}}\,dx\)

Let \(x=3\sin \theta\).

\( \displaystyle \int \dfrac{x}{\sqrt{9-x^{2}}}\,dx=-\sqrt{9-x^{2}}+C\)

Let \(x=3\sin \theta\). Then \(dx=3\cos\theta\) and: \[\begin{aligned} \int \dfrac{x}{\sqrt{9-x^2}} \,dx &= \int \dfrac{3\sin\theta}{3\cos\theta}3\cos\theta\,d\theta \\ &= \int 3\sin\theta\,d\theta \\ &=-3\cos(\theta)+C \\ &=-\sqrt{9-9 \sin^2 \theta} +C \\ &=-\sqrt{9-x^2}+C \end{aligned}\]

pm

\[\begin{aligned} \dfrac{d}{dx}\left(-\sqrt{9-x^2}\right) &=-\dfrac{-2x}{2\sqrt{9-x^2}} \\ &=\dfrac{x}{\sqrt{9-x^2}} \end{aligned}\]

This can also be done by the ordinary substitution \(u=9-x^2\). Then \(du=-2x\,dx\) and so: \[\begin{aligned} \int \dfrac{x}{\sqrt{9-x^{2}}}\;dx &=\int \dfrac{x}{\sqrt{u}}\cdot\dfrac{1}{-2x}\;du =-\int \dfrac{1}{2\sqrt{u}}\;du \\ &=-u^{1/2}+C =-\sqrt{9-x^2}+C\\ \end{aligned}\]
\(\displaystyle \int \dfrac{dx}{x^{2}\sqrt{9-x^{2}}}\)

Recall \(\dfrac{d}{dx}\cot x=-\csc ^{2}x\).

\( \displaystyle \int \dfrac{dx}{x^{2}\sqrt{9-x^{2}}}=-\,\dfrac{\sqrt{9-x^2}}{9x}+C\)

Let \(x=3\sin(\theta)\). Then \(dx=3\cos(\theta)d\theta\). \[\begin{aligned} \int \dfrac{1}{x^2\sqrt{9-x^2}}\,dx &=\int \dfrac{1}{9\sin^2(\theta)\sqrt{9-9\sin^2(\theta)}} 3\cos\theta\,d\theta \\ &=\int \dfrac{3\cos\theta}{9\sin^2(\theta)3\cos\theta} \,d\theta \\ &=\dfrac{1}{9}\int \csc^2(\theta)\,d\theta =-\,\dfrac{1}{9}\cot(\theta)+C \\ &=-\,\dfrac{1}{9}\dfrac{\sqrt{1-\sin^2(\theta)}}{\sin(\theta)}+C\\ &=-\,\dfrac{1}{9}\dfrac{\;\sqrt{1-\dfrac{x^2}{9}}\;}{\dfrac{x}{3}}+C\\ &=-\,\dfrac{\sqrt{9-x^2}}{9x}+C \end{aligned}\]

pm

\[\begin{aligned} \dfrac{d}{dx}\left(-\,\dfrac{\sqrt{9-x^2}}{9x}\right) &=-\,\dfrac{9x(\sqrt{9-x^2})'-\sqrt{9-x^2}9}{81x^2} \\ &=-\,\dfrac{9x\dfrac{-2x}{2\sqrt{9-x^2}}-9\sqrt{9-x^2}}{81x^2} \\ &=\dfrac{9x\dfrac{x}{\sqrt{9-x^2}}+9\sqrt{9-x^2}}{81x^2} \\ &=\dfrac{\dfrac{9x^2}{\sqrt{9-x^2}}+\dfrac{9(9-x^2)}{\sqrt{9-x^2}}}{81x^2} \\ &=\dfrac{81}{81x^2\sqrt{9-x^2}} \\ &=\dfrac{1}{x^2\sqrt{9-x^2}} \end{aligned}\]
\(\displaystyle \int \dfrac{x^{2}}{\sqrt{1-x^{2}}}\,dx \)

Recall the integral of \(\sin^2(x)\) is \(\dfrac{x-\sin(x)\cos(x)}{2}\).

\( \displaystyle \int \dfrac{x^{2}}{\sqrt{1-x^{2}}}\,dx=-\dfrac{1}{2}x\sqrt{1-x^{2}}+\dfrac{1 }{2}\arcsin x+C \)

Let \(x=\sin{\theta}\). Then \(dx=\cos{\theta}\,d\theta\). \[\begin{aligned} \int \dfrac{x^{2}}{\sqrt{1-x^{2}}}\,dx &=\int \dfrac{\sin^2{u}}{\cos{u}} \cos{u}\;du \\ &=\int \sin^2{u}\;du \\ &=\dfrac{u-\sin(u)\cos(u)}{2}+C \\ &=-\dfrac{1}{2}x\sqrt{1-x^{2}}+\dfrac{1}{2}\arcsin x+C \end{aligned}\]

\[\begin{aligned} \dfrac{d}{dx}&\left(-\dfrac{1}{2}x\sqrt{1-x^{2}}+\dfrac{1}{2}\arcsin{x}\right) \\ &=-\dfrac{\sqrt{1-x^2}}{2}-\dfrac{x}{2}\cdot \dfrac{-2x}{2\sqrt{1-x^2}}+\dfrac{1}{2\sqrt{1-x^2}} \\ &=\dfrac{x^2-1}{2\sqrt{1-x^2}}+\dfrac{x^2}{2\sqrt{1-x^2}}+\dfrac{1}{2\sqrt{1-x^2}} \\ &=\dfrac{x^2}{\sqrt{1-x^2}} \end{aligned}\]

Find the area of the surface generated by revolving the graph of \( y=\sqrt{x^{2}+2}\) between \(x=0\) and \(x=1\) about the \(x\)-axis.

It's OK to use the antiderivative of \(\sec^3 x\): \[ \int \sec^3 \theta\,d\theta =\dfrac{1}{2}\sec\theta\tan\theta+\dfrac{1}{2}\ln|\sec\theta+\tan\theta|+C \] which was derived in the chapter on trig integrals.

\(\begin{aligned} A&=\int_{0}^{1} 2\pi \sqrt{x^2+2} \sqrt{1+\left(\dfrac{x}{\sqrt{x^2+2}}\right)^2\,}\,dx \\ &=2\pi +\sqrt{2}\pi \ln \left( \sqrt{2}+1\right) \end{aligned}\)

Since we are revolving about the \(x\)-axis, the radius is \(r=y=\sqrt{x^{2}+2}\). The differential of arclength is \(ds=\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}\,dx\). So the surface area is: \[\begin{aligned} A&=\int_0^1 2\pi y \; ds \\ &=\int_0^1 2\pi \sqrt{x^2+2} \sqrt{1+\left(\dfrac{dy}{dx}\right)^2\,}\,dx \\ &= \int_0^1 2\pi \sqrt{x^2+2} \sqrt{1+\left(\dfrac{x}{\sqrt{x^2+2}}\right)^2\,}\,dx \\ &= \int_0^1 2\pi \sqrt{x^2+2} \sqrt{\dfrac{x^2+2}{x^2+2}+\dfrac{x^2}{x^2+2}\,}\,dx \\ &= 2\sqrt{2} \pi \int_0^1 \sqrt{x^2+1}\,dx \end{aligned}\] We now substitute \(x=\tan(\theta)\) and \(dx=\sec^2(\theta)\,d\theta\). Then we use the integral of \(\sec^3\theta\). (See the hint.) \[\begin{aligned} A&= 2\sqrt{2} \pi \int_0^1 \sqrt{x^2+1}\,dx = 2\sqrt{2} \pi \int_0^{\pi/4} \sec^3(\theta)\,d\theta \\ &=2\sqrt{2}\pi\left[\dfrac{1}{2}\sec(\theta)\tan(\theta)+\dfrac{1}{2}\ln|\sec(\theta)+\tan(\theta)|\right]_0^{\pi/4} \\ &=\sqrt{2}\pi\left[\sec\left(\dfrac{\pi}{4}\right)\tan\left(\dfrac{\pi}{4}\right) +\ln\left|\sec\left(\dfrac{\pi}{4}\right)+\tan\left(\dfrac{\pi}{4}\right)\right|\right. \\ &\qquad\qquad\left.-\sec(0)\tan(0)-\ln\left|\sec(0)+\tan(0)\right|\rule{0pt}{10pt}\right]\\ &=2\sqrt{2}\pi\left[\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}\ln\left(\sqrt{2}+1\right)-\dfrac{1}{2}\ln(1)\right] \\ &=2\pi+\sqrt{2}\pi\ln\left(\sqrt{2}+1\right) \end{aligned}\]